A tiling of 12-fold rotational symmetry from two hexagon grids

We do similarly as in our earlier post “An easy way to quasiperiodic tilings” but now we use grids of hexagons instead of squares. A hexagon has six-fold rotational symmetry and remains unchanged if we rotate it by 60 degrees. We draw two such grids, one rotated by 30 degrees with respect to the other. Thus we get a design, which remains the same if we rotate it by 30 degrees. It thus has 12-fold rotational symmetry but it is not a tiling.

We now search for pairs of hexagons, which form complete 12-pointed stars. Their centers have to lie inside the other hexagon and their corners have to be outside. Each such pair then gives a corner point of the tiling:

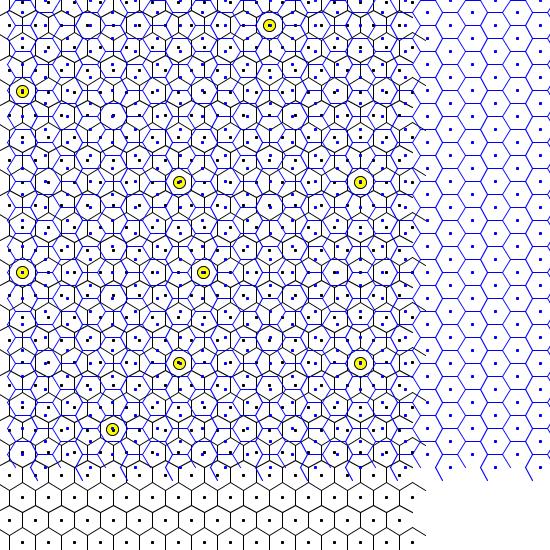
Two hexagon grids. If the centers of two hexagons are sufficiently close to each other they give a corner point (shown as a yellow disc) of the tiling.

These points are then joined by lines of the same length. This gives squares, rhombs with an acute angle of 30 degree and isosceles triangles as tiles. If two rhombs share their sides we have to take care that the computer program will not draw a triangle in the same place. We finally get a tiling, which has been discovered by Stampfli (Helv. Phys. Acta 59, 1260 (1986)) using a much more complicated method:

Quasiperiodic tiling with 12-fold rotational symmetry.

Note the characteristic stars made of 12 rhombs. You can see that they lie at the corners of large squares, rhombs and triangles.  They again form the same quasiperiodic tiling at a much larger scale. Thus this tiling is self-similar as is the Ammann-Beenker tiling.

Quasiperiodicity arises here because the hexagon grids have periodic length of 3 and of the square root of 3 in x-direction, if the length of the sides of the hexagons is equal to one. There is no common period because the square root of three is an irrational number. However, finite parts of the tiling are repeated throughout.